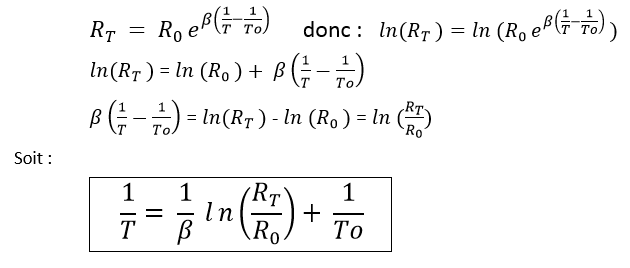” Etalonnage d’une thermistance CTN ”

. Objectif

Dans notre laboratoire, nous avons trouvé une thermistance ne portant aucune indication et dont nous ne disposons pas de la fiche technique (datasheet) du fabricant.

L’objectif de cette activité est d’étalonner cette thermistance à l’aide d’un capteur de température TMP 36 ou LM 35.

Pour cela, nous allons faire varier la température et on va demander à l’Arduino de mesurer la résistance de la thermistance en fonction de la température qui sera mesurée en parallèle par le capteur.

On pourra alors tracer la caractéristique résistance/température qui permettra après de mesurer n’importe quelle température avec cette thermistance grâce à la mesure de sa résistance.

 

. Le montage

 

 

. Les thermistances

Les thermistances, composées d’un matériau semi-conducteur, combinaison de métaux et de matériaux à base d’oxyde métallique (oxyde de manganèse, cobalt, cuivre et nickel), sont des capteurs de température résistifs, dont la résistance varie de façon importante et non linéaire quand la température change même faiblement.

On distingue deux types de thermistances : les CTN et les CTP.

– Les CTN (Coefficient de Température Négatif, en anglais NTC, Negative Temperature Coefficient) sont des thermistances dont la résistance diminue quand la température augmente :

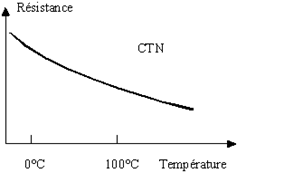
– Les CTP (Coefficient de Température Positif, en anglais PTC, Positive Temperature Coefficient) sont des thermistances, fabriquées à base de titanate de baryum, dont la résistance augmente fortement avec la température dans une plage de température limitée (typiquement entre 0 °C et 100 °C), mais diminue en dehors de cette zone :

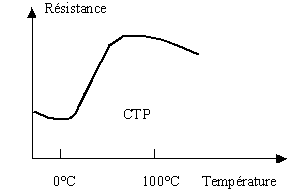
Le symbole des thermistances est basé sur celui d’une résistance variable :

 

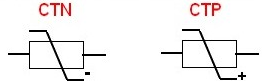
Même si la variation de résistance en fonction de la température d’une thermistance n’est pas linéaire, il est tout à fait possible de l’utiliser pour faire des mesures de température avec une grande précision si la loi de variation est connue, notamment avec une CTN.

En effet, Quand l’effet Joule (échauffement dû au passage du courant) est négligeable, on peut exprimer une relation entre la résistance de la CTN et sa température par la relation de Steinhart-Hart :

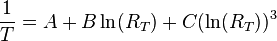
Cette formule, valable à toutes les températures, peut être simplifiée sur une plage limitée de températures. La formule devient :

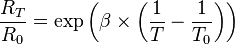
La principale caractéristique d’une CTN ou d’une CTP est la valeur de la résistance R₀ (en Ω) à la température de 25°C.

Le plus souvent, le marquage du composant indique la valeur de R₀. Il s’agit d’un nombre à 3 chiffres, les 2 premiers chiffres représente la valeur, le 3ème chiffre le coefficient multiplicateur en puissance de 10 :

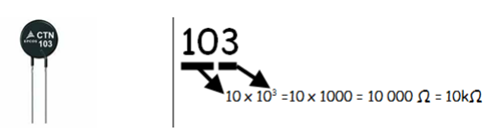
Avec un Arduino, On utilise la thermistance dans un montage (Cf. ci-dessous), avec une résistance fixe de 10 kΩ, qu’on appelle un diviseur de tension.

 

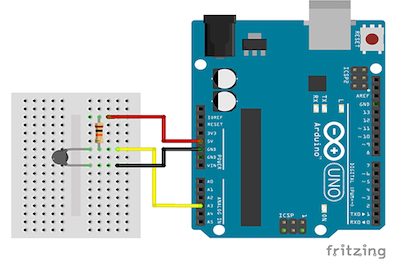
La thermistance est alimentée en 5V depuis l’Arduino. Le point entre les deux résistances est relié à une broche analogique de l’Arduino et on mesure la tension de cette broche par la fonction “analogRead (broche)”.

 Diviseur de tension :

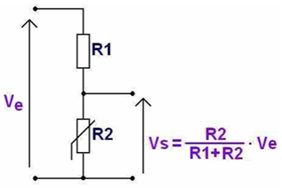
En fonction de la température (T), la valeur de la thermistance R2 varie, ce qui modifie le courant qui circule dans le circuit et donc la tension Vs aux bornes de R2.

La résistance R1 de 10kΩ, elle a pour rôle de limiter le courant circulant dans le montage.

La tension Ve est fournie par l’ARDUINO et vaut 5V.

Vs est la tension mesurée par le microcontrôleur. On peut alors calculée R2 :

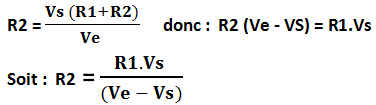
Et tracer la caractéristique R2 = f(T).

 

. Le programme

Voici le code de l’activité :

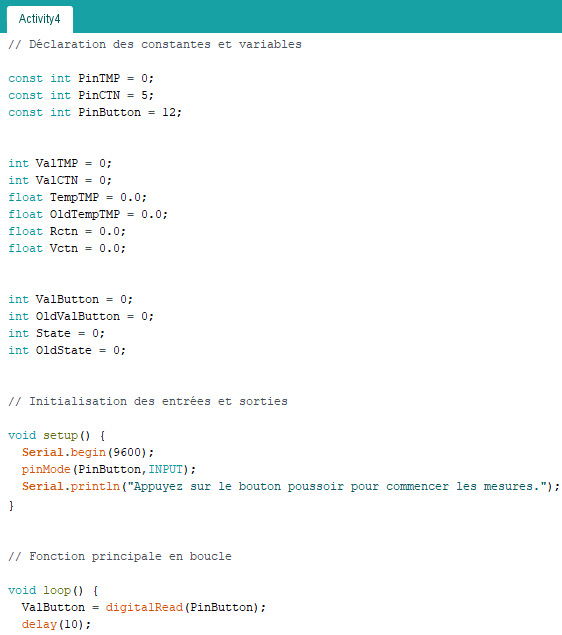
Déroulement du programme :

– Déclaration des constantes et variables :

. const int PinTMP = 0   (variable nombre entier correspondant à la broche du capteur de température TMP 36)

. const int PinCTN = 5   (variable nombre entier correspondant à la broche de la CTN)

. const int PinButton = 12   (variable nombre entier correspondant à la broche du bouton poussoir)

. int ValTMP = 0   (variable nombre entier pour stocker la valeur de la broche du TMP 36)

. int ValCTN = 0   (variable nombre entier pour stocker la valeur de la broche de la CTN)

. float TempTMP = 0.0   (variable nombre décimal pour stocker le résultat du calcul de la température)

. float OldTempTMP = 0.0   (variable nombre décimal pour stocker le résultat du calcul de température précédent)

. float Rctn = 0.0    (variable nombre décimal pour stocker le résultat du calcul de la résistance de la CTN)

. float Vctn = 0.0    (variable nombre décimal pour stocker le résultat du calcul de la tension de la broche de la CTN)

. int ValButton = 0    (variable nombre entier pour stocker la valeur de la broche du bouton poussoir)

. int OldValButton = 0    (variable nombre entier pour stocker la valeur précédente de la broche du bouton poussoir)

. int State = 0     (variable nombre entier correspondant à l’action à effectuer)

. int OldState = 0    (variable nombre entier correspondant à l’action effectuée précédemment)

 

– Initialisation des entrées et sorties :

. Initialisation de la liaison série à un débit de 9600 bauds

. Initialisation de la broche du bouton poussoir en entrée

 

– Fonction principale en boucle :

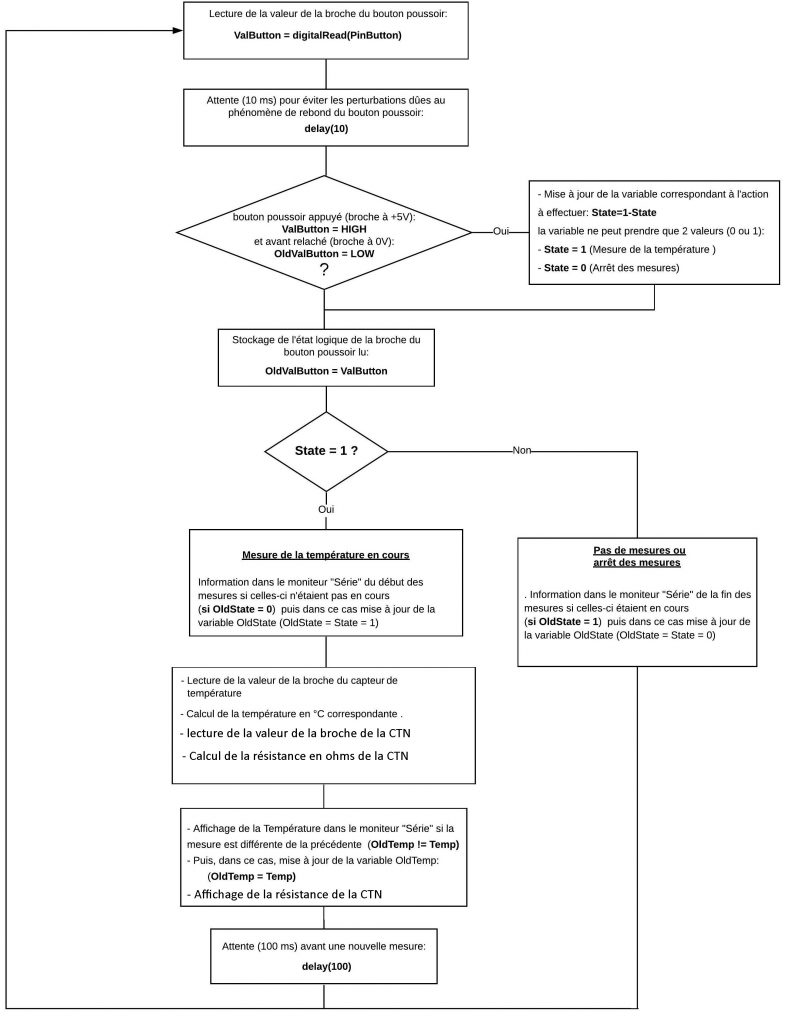
Résultats dans le moniteur série :

 

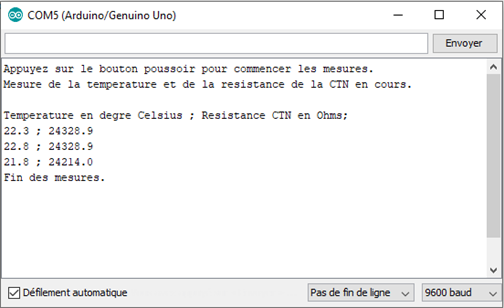
. Exploitation des mesures

En chauffant progressivement le bain-marie, on relève la température (T) donnée par le capteur TMP 36 et la résistance (Rt) de la CTN. Puis on trace la caractéristique Rt = f(T) :

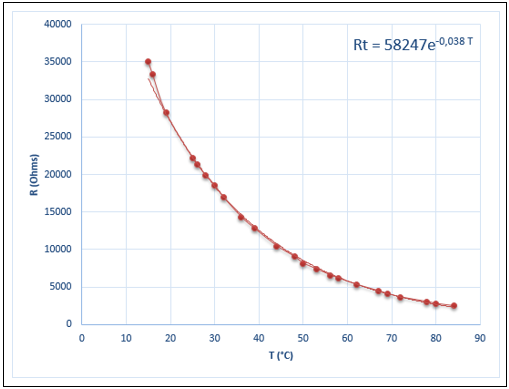
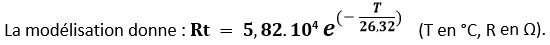
On en déduit alors l’expression de la température en fonction de la résistance de la CTN, dans la plage de températures de l’expérience :

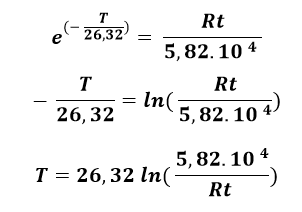
Ainsi, avec l’Arduino, pour n’importe quelle température dans la plage de l’expérience, par mesure de la résistance de la CTN, on pourra déterminer la température correspondante.

 

On peut également modéliser la caractéristique Rt = f(T) de notre CTN avec la relation simplifiée de Steinhart-Hart  (T en K):

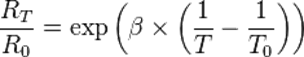
A partir du graphe, on détermine une des deux grandeurs caractéristiques de la CTN:

–> à T₀ = 298,15 K,  R₀ = 22,2 kΩ

La modélisation suivant cette relation à l’aide du logiciel Régressi donne la valeur de β (en K) :

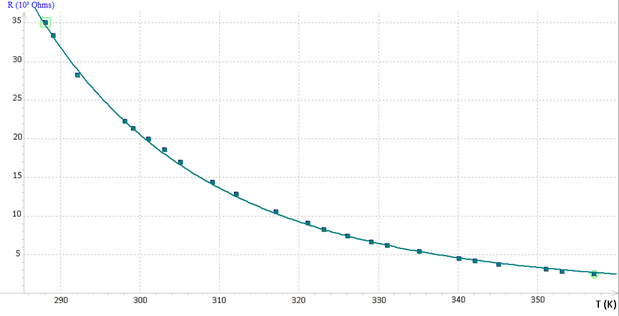
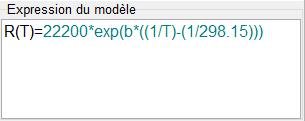
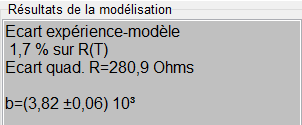
Dans la plage de températures de l’expérience, la relation simplifiée de Steinhart-Hart est vérifiée. On trouve : β = 3820 K

On en déduit alors l’expression de la température (en K) en fonction de la résistance de la CTN (en Ohms) :