” Charge & Décharge ”
(Cliquez pour afficher la version PDF)

. Les condensateurs
Un condensateur est un composant électronique capable de stocker de l’énergie sous la forme d’un champ électrostatique. Il est constitué de 2 armatures séparées par un isolant, le ”diélectrique”.
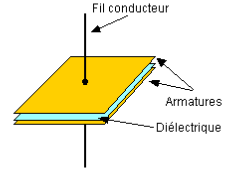
Les dimensions des armatures (ou plaques) sont grandes devant l’épaisseur de l’isolant. Par commodité, les films métalliques et l’isolant sont enroulés ou juxtaposés en plusieurs couches.
Dans les schémas de circuits électriques, le condensateur est symbolisé par :
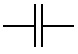
Les condensateurs avec un diélectrique chimique sont polarisés.
Ils sont représentés par ce symbole :
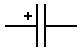
Les condensateurs polarisés possèdent un pôle « plus » et un pôle « moins », ils doivent impérativement être connectés dans le bon sens. En règle générale, les condensateurs polarisés radiaux (qui ont les deux pattes du même côté) possèdent une bande ou un ensemble de flèches qui désigne le pôle négatif, et les condensateurs polarisés axiaux (qui ont les deux pattes opposées) possèdent un renfoncement (collerette) côté pôle positif :
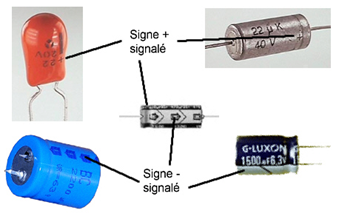
La caractéristique principale d’un condensateur est sa capacité exprimée en farad.
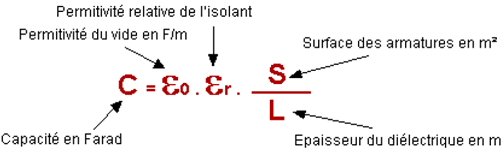
En appliquant, une tension U aux bornes d’un condensateur, il apparait une charge q, sur une de ses plaques, proportionnelle à la tension appliquée.
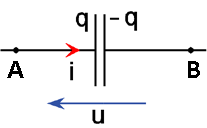
La charge qui apparaît sur l’une des plaques est l’opposé de celle qui apparaît sur l’autre plaque.
En effet, la conservation de la charge électrique s’écrit : q + q’ = 0
d’où: q’ = − q.
La charge q est, par convention la charge portée par la plaque par laquelle on entre dans le condensateur. On a alors :
q = C.U
où : q est exprimé en coulomb (C), U en volt (V) et C en Farad (F)
Remarque : Le farad étant une grande unité, on utilise souvent des sous-multiples :
1 µF = 10-6 F, 1 nF = 10−9 F, 1 pF = 10−12 F
L’intensité du courant, i, est le débit de charges et est égale à la quantité de charges qui passent par unité de temps à travers une section de conducteur :
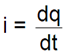
On oriente géométriquement le condensateur de la borne A vers la borne B.
Soit iAB l’intensité algébrique du courant allant de A vers B et qA la charge qui apparaît sur la plaque par laquelle on entre dans le condensateur.
On a donc : qA = − qB = C.(VA − VB)
En tenant compte de la relation entre iAB et qA, on a :
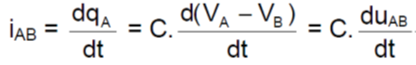
On retiendra les relations suivantes :
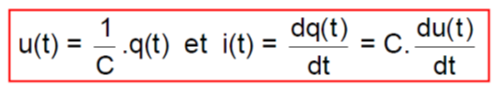
. Le dipôle RC
Un dipôle RC est l’association en série d’un conducteur ohmique (conducteur ohmique) de résistance R et d’un condensateur de capacité C, comme dans le schéma ci-dessous :
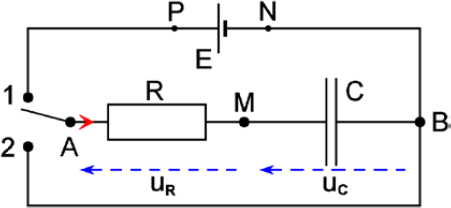
1. Charge du condensateur
Le condensateur étant déchargé, on bascule, à l’instant t=0, l’interrupteur en position 1.
A chaque instant t > 0, on a :
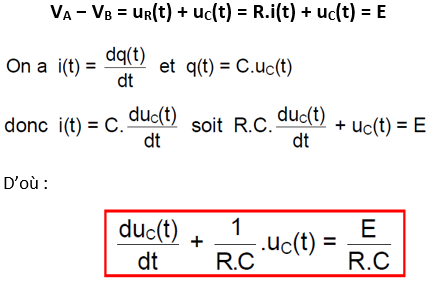




2. Décharge du condensateur dans une résistance
Le condensateur étant chargé, on bascule, à l’instant t=0, l’interrupteur en position 2.




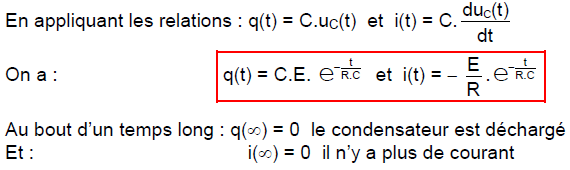
3. Constante de temps du dipôle RC
Le produit R.C est homogène à un temps et est appelé constante de temps τ du dipôle RC.
. Lors de la charge :
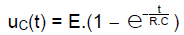
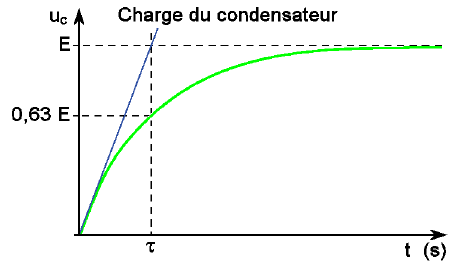

Et :
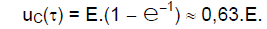
Par lecture graphique de l’abscisse du point de la courbe dont l’ordonnée est égale à 0,63.E, on obtient la valeur de τ.
. Lors de la décharge :
![]()
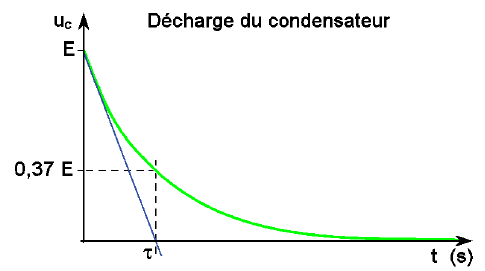
La tangente à la courbe, à t=0s, coupe l’asymptote y=0 au point d’abscisse t = τ.
En effet, la tangente à la courbe représentative de uc(t), à t = 0 s, a pour équation :
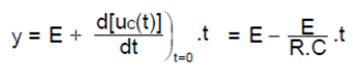
Si t = τ = R.C , on a alors : y = 0
On a également :
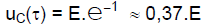
Par lecture graphique de l’abscisse du point de la courbe dont l’ordonnée est égale à 0,37.E, on obtient la valeur de τ.
. Les activités
- Activité 1: Etude de la charge d’un condensateur d’un dipôle RC
- Activité 2: Etude de la décharge d’un condensateur d’un dipôle RC
- Activité 3: Détermination de la capacité d’un condensateur par mesure d’une constante de temps
- Activité 4: Simulation d’un flash photographique
- Activité 5: Réaliser un flash périodique

